본문 바로가기
DSA

다항식 계산기 (Polynomial Calculator)

by KWONE 2024. 10. 2.

 

#include <stdio.h>
#include <stdlib.h>

#define MAX_DEGREE 101

typedef struct {
    int degree;               // 최대 차수
    float x_coef[MAX_DEGREE]; // x 계수 배열
    float y_coef[MAX_DEGREE]; // y 계수 배열
} polynomial;

typedef struct {
    int x_exp;  // x의 차수
    int y_exp;  // y의 차수
    float coef; // 항의 계수
} term;

int compare(const void* a, const void* b) {
    term* termA = (term*)a;
    term* termB = (term*)b;

    if (termB->y_exp != termA->y_exp) {
        return termB->y_exp - termA->y_exp;
    }
    else {
        return termB->x_exp - termA->x_exp;
    }
}

void combineLikeTerms(term* resultPoly, int* term_count) {
    int count = 0;

    for (int i = 0; i < *term_count - 1; i++) {
        if (resultPoly[i].coef == 0) continue;

        for (int j = i + 1; j < *term_count; j++) {
            if (resultPoly[i].x_exp == resultPoly[j].x_exp && resultPoly[i].y_exp == resultPoly[j].y_exp) {
                resultPoly[i].coef += resultPoly[j].coef;
                resultPoly[j].coef = 0; 
            }
        }
    }
    for (int i = 0; i < *term_count; i++) {
        if (resultPoly[i].coef != 0) {
            resultPoly[count++] = resultPoly[i];
        }
    }
    *term_count = count;
}

void multiPoly(polynomial a, polynomial b, term* resultPoly, int* term_count) {
    int count = 0;

    for (int i = 0; i <= a.degree; i++) {
        for (int j = 0; j <= b.degree; j++) {
            if ((a.x_coef[i] != 0 || a.y_coef[i] != 0) && (b.x_coef[j] != 0 || b.y_coef[j] != 0)) {
                // x항
                if (a.x_coef[i] != 0 && b.x_coef[j] != 0) {
                    resultPoly[count].coef = a.x_coef[i] * b.x_coef[j];
                    resultPoly[count].x_exp = i + j;
                    resultPoly[count].y_exp = 0;
                    count++;
                }
                // y항
                if (a.y_coef[i] != 0 && b.y_coef[j] != 0) {
                    resultPoly[count].coef = a.y_coef[i] * b.y_coef[j];
                    resultPoly[count].x_exp = 0;
                    resultPoly[count].y_exp = i + j;
                    count++;
                }
                // x*y 혼합 항
                if (a.x_coef[i] != 0 && b.y_coef[j] != 0) {
                    resultPoly[count].coef = a.x_coef[i] * b.y_coef[j];
                    resultPoly[count].x_exp = i;
                    resultPoly[count].y_exp = j;
                    count++;
                }
                if (a.y_coef[i] != 0 && b.x_coef[j] != 0) {
                    resultPoly[count].coef = a.y_coef[i] * b.x_coef[j];
                    resultPoly[count].x_exp = j;
                    resultPoly[count].y_exp = i;
                    count++;
                }
            }
        }
    }
    *term_count = count;

    combineLikeTerms(resultPoly, term_count);
}

void printResult(term* terms, int term_count) {
    int first = 1;
    for (int i = 0; i < term_count; i++) {
        if (terms[i].coef == 0) continue; // 계수가 0인 항은 생략
        if (!first && terms[i].coef > 0) {
            printf("+");
        }
        if (terms[i].y_exp == 0 && terms[i].x_exp == 0) {
            printf("%.1f", terms[i].coef);
        }
        else if (terms[i].y_exp == 0) {
            printf("%.1fx^%d", terms[i].coef, terms[i].x_exp);
        }
        else if (terms[i].x_exp == 0) {
            printf("%.1fy^%d", terms[i].coef, terms[i].y_exp);
        }
        else {
            printf("%.1fy^%dx^%d", terms[i].coef, terms[i].y_exp, terms[i].x_exp);
        }

        first = 0;
    }
    printf("\n");
}

void initPoly(polynomial* p, const char* input) {
    p->degree = 0;
    for (int i = 0; i < MAX_DEGREE; i++) {
        p->x_coef[i] = 0;
        p->y_coef[i] = 0;
    }

    int sign = 1; //부호
    float coef = 0; 
    int degree = 0; 
    int i = 0;

    while (input[i] != '\0' && input[i] != '\n') {
        if (input[i] == '+' || input[i] == '-') {
            sign = (input[i] == '-') ? -1 : 1;
            i++;
        }

        coef = 0;
        while (input[i] >= '0' && input[i] <= '9') {
            coef = coef * 10 + (input[i] - '0');
            i++;
        }
        coef *= sign;

        if (input[i] == 'x' || input[i] == 'y') {
            char variable = input[i];
            i++;
            degree = 0; // 기본 차수는 0
            if (input[i] == '^') {
                i++;
                while (input[i] >= '0' && input[i] <= '9') {
                    degree = degree * 10 + (input[i] - '0');
                    i++;
                }
            }
            else {
                degree = 1; // 기본 차수는 1
            }
            if (variable == 'x') {
                p->x_coef[degree] += coef;
            }
            else if (variable == 'y') {
                p->y_coef[degree] += coef;
            }
            if (degree > p->degree) {
                p->degree = degree;
            }
        }
        else {
            p->x_coef[0] += coef; 
        }
    }
}

int main() {
    term resultPoly[MAX_DEGREE];
    int term_count;
    char input1[1000];
    char input2[1000];
    polynomial a1;
    polynomial b1;

    while (1) {
        printf("다항식을 입력하시오: (0 입력시 종료)\n");

        printf("A 다항식: ");
        fgets(input1, sizeof(input1), stdin);
        if (input1[0] == '0' && input1[1] == '\n') {
            printf("0을 입력해서 종료합니다.\n");
            break;
        }
        initPoly(&a1, input1);

        printf("B 다항식: ");
        fgets(input2, sizeof(input2), stdin);
        if (input1[0] == '0' && input1[1] == '\n') {
            printf("0을 입력해서 종료합니다.\n");
            break;
        }
        initPoly(&b1, input2);

        multiPoly(a1, b1, resultPoly, &term_count);
        qsort(resultPoly, term_count, sizeof(term), compare);
        printf("결과 다항식: ");
        printResult(resultPoly, term_count);

        printf("-----------------------------------------------------------------------------------------------\n");
    }

    return 0;
}

다항식을 입력하시오: (0 입력시 종료)
A 다항식: 3y^7+4x^4-1
B 다항식: 5x^4-3y^2+7
결과 다항식: -9.0y^9+15.0x^4y^7+21.0y^7-12.0x^4y^2+3.0y^2+20.0x^8+23.0x^4-7.0
-----------------------------------------------------------------------------------------------
다항식을 입력하시오: (0 입력시 종료)
A 다항식: 4y^7-4x^4-1
B 다항식: 2y^7-3x+1
결과 다항식: 8.0y^14-8.0x^4y^7-12.0x^1y^7+2.0y^7+12.0x^5-4.0x^4+3.0x^1-1.0
-----------------------------------------------------------------------------------------------

#include <stdio.h>
#include <stdlib.h>

#define MAX_DEGREE 101

typedef struct {
    int degree;               // 최대 차수
    float x_coef[MAX_DEGREE]; // x 계수 배열
    float y_coef[MAX_DEGREE]; // y 계수 배열
} polynomial;

typedef struct {
    int x_exp;  // x의 차수
    int y_exp;  // y의 차수
    float coef; // 항의 계수
} term;

int compare(const void* a, const void* b) {
    term* termA = (term*)a;
    term* termB = (term*)b;

    if (termB->y_exp != termA->y_exp) {
        return termB->y_exp - termA->y_exp;
    }
    else {
        return termB->x_exp - termA->x_exp;
    }
}

void multiPoly(polynomial a, polynomial b, term* resultPoly, int* term_count) {
    int count = 0;

    for (int i = 0; i <= a.degree; i++) {
        for (int j = 0; j <= b.degree; j++) {
            if ((a.x_coef[i] != 0 || a.y_coef[i] != 0) && (b.x_coef[j] != 0 || b.y_coef[j] != 0)) {
                // x항
                if (a.x_coef[i] != 0 && b.x_coef[j] != 0) {
                    resultPoly[count].coef = a.x_coef[i] * b.x_coef[j];
                    resultPoly[count].x_exp = i + j;
                    resultPoly[count].y_exp = 0;
                    count++;
                }
                // y항
                if (a.y_coef[i] != 0 && b.y_coef[j] != 0) {
                    resultPoly[count].coef = a.y_coef[i] * b.y_coef[j];
                    resultPoly[count].x_exp = 0;
                    resultPoly[count].y_exp = i + j;
                    count++;
                }
                // x*y혼합 항
                if (a.x_coef[i] != 0 && b.y_coef[j] != 0) {
                    resultPoly[count].coef = a.x_coef[i] * b.y_coef[j];
                    resultPoly[count].x_exp = i;
                    resultPoly[count].y_exp = j;
                    count++;
                }
                if (a.y_coef[i] != 0 && b.x_coef[j] != 0) {
                    resultPoly[count].coef = a.y_coef[i] * b.x_coef[j];
                    resultPoly[count].x_exp = j;
                    resultPoly[count].y_exp = i;
                    count++;
                }
            }
        }
    }
    *term_count = count;
}

void printResult(term* terms, int term_count) {
    int first = 1;
    for (int i = 0; i < term_count; i++) {
        if (terms[i].coef == 0) continue; // 계수가 0인 항은 생략
        if (!first && terms[i].coef > 0) {
            printf("+");
        }
        if (terms[i].y_exp == 0 && terms[i].x_exp == 0) {
            printf("%.1f", terms[i].coef);
        }
        else if (terms[i].y_exp == 0) {
            printf("%.1fx^%d", terms[i].coef, terms[i].x_exp);
        }
        else if (terms[i].x_exp == 0) {
            printf("%.1fy^%d", terms[i].coef, terms[i].y_exp);
        }
        else {
            printf("%.1fy^%dx^%d", terms[i].coef, terms[i].y_exp, terms[i].x_exp);
        }

        first = 0;
    }
    printf("\n");
}
void initPoly(polynomial* p, const char* input) {
    p->degree = 0;
    for (int i = 0; i < MAX_DEGREE; i++) {
        p->x_coef[i] = 0;
        p->y_coef[i] = 0;
    }

    int sign = 1; // 계수의 부호
    float coef = 0; // 계수
    int degree = 0; // 차수
    int i = 0; // 인덱스

    while (input[i] != '\0' && input[i] != '\n') {
        // 부호 처리
        if (input[i] == '+' || input[i] == '-') {
            sign = (input[i] == '-') ? -1 : 1;
            i++;
        }

        coef = 0;
        while (input[i] >= '0' && input[i] <= '9') {
            coef = coef * 10 + (input[i] - '0');
            i++;
        }
        coef *= sign;

        // 변수 처리
        if (input[i] == 'x' || input[i] == 'y') {
            char variable = input[i];
            i++;
            degree = 0; // 기본 차수는 0
            if (input[i] == '^') {
                i++;
                while (input[i] >= '0' && input[i] <= '9') {
                    degree = degree * 10 + (input[i] - '0');
                    i++;
                }
            }
            else {
                degree = 1; // 기본 차수는 1
            }
            if (variable == 'x') {
                p->x_coef[degree] += coef;
            }
            else if (variable == 'y') {
                p->y_coef[degree] += coef;
            }
            if (degree > p->degree) {
                p->degree = degree;
            }
        }
        else {
            // 상수항 처리
            p->x_coef[0] += coef; // 상수항을 x 계수에 저장
        }
    }
}

int main() {
    term resultPoly[MAX_DEGREE];
    int term_count;
    char input1[1000];
    char input2[1000];
    polynomial a1; 
    polynomial b1; 
  
    while (1) {
        printf("다항식을 입력하시오: (0 입력시 종료)\n");

        printf("A 다항식: ");
        fgets(input1, sizeof(input1), stdin);
        if (strcmp(input1, "0\n") == 0) { 
            printf("0을 입력해서 종료합니다.\n");
            break;
        }
        initPoly(&a1, input1);  

        printf("B 다항식: ");
        fgets(input2, sizeof(input2), stdin);
        if (strcmp(input2, "0\n") == 0) {  
            printf("0을 입력해서 종료합니다.\n");
            break;
        }
        initPoly(&b1, input2);  

        multiPoly(a1, b1, resultPoly, &term_count);
        qsort(resultPoly, term_count, sizeof(term), compare);
        printf("결과 다항식: ");
        printResult(resultPoly, term_count);

        printf("-----------------------------------------------------------------------------------------------\n");
    }

    return 0;
}

 

 

#include <stdio.h>
#include <stdlib.h>

#define MAX_DEGREE 101

typedef struct {
    int degree;               // 최대 차수
    float x_coef[MAX_DEGREE]; // x 계수 배열
    float y_coef[MAX_DEGREE]; // y 계수 배열
} polynomial;

typedef struct {
    int x_exp;  // x의 차수
    int y_exp;  // y의 차수
    float coef; // 항의 계수
} term;

int compare(const void* a, const void* b) {
    term* termA = (term*)a;
    term* termB = (term*)b;

    if (termB->y_exp != termA->y_exp) {
        return termB->y_exp - termA->y_exp;
    }
    else {
        return termB->x_exp - termA->x_exp;
    }
}

void multiPoly(polynomial a, polynomial b, term* resultPoly, int* term_count) {
    int count = 0;

    for (int i = 0; i <= a.degree; i++) {
        for (int j = 0; j <= b.degree; j++) {
            if ((a.x_coef[i] != 0 || a.y_coef[i] != 0) && (b.x_coef[j] != 0 || b.y_coef[j] != 0)) {
                // x항
                if (a.x_coef[i] != 0 && b.x_coef[j] != 0) {
                    resultPoly[count].coef = a.x_coef[i] * b.x_coef[j];
                    resultPoly[count].x_exp = i + j;
                    resultPoly[count].y_exp = 0;
                    count++;
                }
                // y항
                if (a.y_coef[i] != 0 && b.y_coef[j] != 0) {
                    resultPoly[count].coef = a.y_coef[i] * b.y_coef[j];
                    resultPoly[count].x_exp = 0;
                    resultPoly[count].y_exp = i + j;
                    count++;
                }
                // x*y혼합 항
                if (a.x_coef[i] != 0 && b.y_coef[j] != 0) {
                    resultPoly[count].coef = a.x_coef[i] * b.y_coef[j];
                    resultPoly[count].x_exp = i;
                    resultPoly[count].y_exp = j;
                    count++;
                }
                if (a.y_coef[i] != 0 && b.x_coef[j] != 0) {
                    resultPoly[count].coef = a.y_coef[i] * b.x_coef[j];
                    resultPoly[count].x_exp = j;
                    resultPoly[count].y_exp = i;
                    count++;
                }
            }
        }
    }
    *term_count = count;
}

void printResult(term* terms, int term_count) {
    int first = 1;
    for (int i = 0; i < term_count; i++) {
        if (terms[i].coef == 0) continue; // 계수가 0인 항은 생략
        if (!first && terms[i].coef > 0) {
            printf("+");
        }
        if (terms[i].y_exp == 0 && terms[i].x_exp == 0) {
            printf("%.1f", terms[i].coef);
        }
        else if (terms[i].y_exp == 0) {
            printf("%.1fx^%d", terms[i].coef, terms[i].x_exp);
        }
        else if (terms[i].x_exp == 0) {
            printf("%.1fy^%d", terms[i].coef, terms[i].y_exp);
        }
        else {
            printf("%.1fy^%dx^%d", terms[i].coef, terms[i].y_exp, terms[i].x_exp);
        }

        first = 0;
    }
    printf("\n");
}
void initPoly(polynomial* p, const char* input) {
    p->degree = 0;
    for (int i = 0; i < MAX_DEGREE; i++) {
        p->x_coef[i] = 0;
        p->y_coef[i] = 0;
    }

    int sign = 1; // 계수의 부호
    float coef = 0; // 계수
    int degree = 0; // 차수
    int i = 0; // 인덱스

    while (input[i] != '\0' && input[i] != '\n') {
        // 부호 처리
        if (input[i] == '+' || input[i] == '-') {
            sign = (input[i] == '-') ? -1 : 1;
            i++;
        }

        coef = 0;
        while (input[i] >= '0' && input[i] <= '9') {
            coef = coef * 10 + (input[i] - '0');
            i++;
        }
        coef *= sign;

        // 변수 처리
        if (input[i] == 'x' || input[i] == 'y') {
            char variable = input[i];
            i++;
            degree = 0; // 기본 차수는 0
            if (input[i] == '^') {
                i++;
                while (input[i] >= '0' && input[i] <= '9') {
                    degree = degree * 10 + (input[i] - '0');
                    i++;
                }
            }
            else {
                degree = 1; // 기본 차수는 1
            }
            if (variable == 'x') {
                p->x_coef[degree] += coef;
            }
            else if (variable == 'y') {
                p->y_coef[degree] += coef;
            }
            if (degree > p->degree) {
                p->degree = degree;
            }
        }
        else {
            // 상수항 처리
            p->x_coef[0] += coef; // 상수항을 x 계수에 저장
        }
    }
}

int main() {
    term resultPoly[MAX_DEGREE];
    int term_count;
    char input1[1000];
    char input2[1000];
    polynomial a1; 
    polynomial b1; 
  
    do {
        printf("다항식을 입력하시오: (0 입력시 종료)\n");
        printf("A 다항식: ");
        fgets(input1, sizeof(input1), stdin);
        initPoly(&a1, input1);
        printf("B 다항식: ");
        fgets(input2, sizeof(input2), stdin);
        initPoly(&b1, input2);

        multiPoly(a1, b1, resultPoly, &term_count);
        qsort(resultPoly, term_count, sizeof(term), compare);
        printf("결과 다항식: ");
        printResult(resultPoly, term_count);
        printf("-----------------------------------------------------------------------------------------------\n");
    } while (input1 == 0||input2==0);
    

    printf("0을 입력하여 종료합니다.");
    return 0;
}

 

 

 

#include <stdio.h>
#include <stdlib.h>

#define MAX_DEGREE 101

typedef struct {
    int degree;               // 최대 차수
    float x_coef[MAX_DEGREE]; // x 계수 배열
    float y_coef[MAX_DEGREE]; // y 계수 배열
} polynomial;

typedef struct {
    int x_exp;  // x의 차수
    int y_exp;  // y의 차수
    float coef; // 항의 계수
} term;

int compare(const void* a, const void* b) {
    term* termA = (term*)a;
    term* termB = (term*)b;

    if (termB->y_exp != termA->y_exp) {
        return termB->y_exp - termA->y_exp;
    }
    else {
        return termB->x_exp - termA->x_exp;
    }
}

void multiPoly(polynomial a, polynomial b, term* resultPoly, int* term_count) {
    int count = 0;

    for (int i = 0; i <= a.degree; i++) {
        for (int j = 0; j <= b.degree; j++) {
            if ((a.x_coef[i] != 0 || a.y_coef[i] != 0) && (b.x_coef[j] != 0 || b.y_coef[j] != 0)) {
                // x 항 곱하기
                if (a.x_coef[i] != 0 && b.x_coef[j] != 0) {
                    resultPoly[count].coef = a.x_coef[i] * b.x_coef[j];
                    resultPoly[count].x_exp = a.degree - i + b.degree - j;
                    resultPoly[count].y_exp = 0;
                    count++;
                }
                // y 항 곱하기
                if (a.y_coef[i] != 0 && b.y_coef[j] != 0) {
                    resultPoly[count].coef = a.y_coef[i] * b.y_coef[j];
                    resultPoly[count].x_exp = 0;
                    resultPoly[count].y_exp = a.degree - i + b.degree - j;
                    count++;
                }
                // x*y 혼합 항 곱하기
                if (a.x_coef[i] != 0 && b.y_coef[j] != 0) {
                    resultPoly[count].coef = a.x_coef[i] * b.y_coef[j];
                    resultPoly[count].x_exp = a.degree - i;
                    resultPoly[count].y_exp = b.degree - j;
                    count++;
                }
                if (a.y_coef[i] != 0 && b.x_coef[j] != 0) {
                    resultPoly[count].coef = a.y_coef[i] * b.x_coef[j];
                    resultPoly[count].x_exp = b.degree - j;
                    resultPoly[count].y_exp = a.degree - i;
                    count++;
                }
            }
        }
    }
    *term_count = count;
}

void printResult(term* terms, int term_count) {
    int first = 1;
    for (int i = 0; i < term_count; i++) {
        if (terms[i].coef == 0) continue; // 계수가 0인 항은 생략

        // 부호 출력
        if (!first && terms[i].coef > 0) {
            printf("+");
        }

        // 상수항 처리
        if (terms[i].y_exp == 0 && terms[i].x_exp == 0) {
            printf("%.1f", terms[i].coef);  // 상수 출력
        }
        else if (terms[i].y_exp == 0) {
            printf("%.1fx^%d", terms[i].coef, terms[i].x_exp);  // y^0 생략
        }
        else if (terms[i].x_exp == 0) {
            printf("%.1fy^%d", terms[i].coef, terms[i].y_exp);  // x^0 생략
        }
        else {
            printf("%.1fy^%dx^%d", terms[i].coef, terms[i].y_exp, terms[i].x_exp);
        }

        first = 0;
    }
    printf("\n");
}

void printPoly(polynomial poly) {
    int first = 1;  // 첫 번째 항 여부
    for (int i = 0; i <= poly.degree; i++) {
        // x 계수 출력
        if (poly.x_coef[i] != 0) {
            // 부호 출력
            if (!first && poly.x_coef[i] > 0) {
                printf("+");
            }

            // x^0 생략 처리
            if (i == poly.degree) {  // 상수항인 경우
                printf("%.1f", poly.x_coef[i]);  // x^0은 그냥 계수 출력
            }
            else {
                printf("%.1fx^%d", poly.x_coef[i], poly.degree - i);
            }
            first = 0;  // 첫 번째 항 이후
        }

        // y 계수 출력
        if (poly.y_coef[i] != 0) {
            // 부호 출력
            if (!first && poly.y_coef[i] > 0) {
                printf("+");
            }

            // y^0 생략 처리
            if (i == poly.degree) {  // 상수항인 경우
                printf("%.1f", poly.y_coef[i]);  // y^0은 그냥 계수 출력
            }
            else {
                printf("%.1fy^%d", poly.y_coef[i], poly.degree - i);
            }
            first = 0;  // 첫 번째 항 이후
        }
    }
    printf("\n");
}


int main() {
    term resultPoly[MAX_DEGREE];
    int term_count;

    polynomial a1 = { 7, {0, 0, 0, 4, 0, 0, 0, -1}, {3, 0, 0, 0, 0, 0, 0, 0} };
    polynomial b1 = { 4, {5, 0, 0, 0, 7}, {0, 0, -3, 0, 0} };

    printf("A 다항식: ");
    printPoly(a1);
    printf("B 다항식: ");
    printPoly(b1);

    multiPoly(a1, b1, resultPoly, &term_count);
    qsort(resultPoly, term_count, sizeof(term), compare);
    printf("결과 다항식: ");
    printResult(resultPoly, term_count);

    printf("-----------------------------------------------------------------------------------------------\n");
    polynomial a2 = { 7,{0,0,0,-4,0,0,0,-1},{4,0,0,0,0,0,0,0} };
    polynomial b2 = { 7,{0,0,0,0,0,0,-3,1},{2,0,0,0,0,0,0,0} };

    printf("A 다항식: ");
    printPoly(a2);
    printf("B 다항식: ");
    printPoly(b2);

    multiPoly(a2, b2, resultPoly, &term_count);
    qsort(resultPoly, term_count, sizeof(term), compare);
    printf("결과 다항식: ");
    printResult(resultPoly, term_count);

    printf("-----------------------------------------------------------------------------------------------\n");
   
    return 0;
}

 

#include <stdio.h>
#include <stdlib.h>

#define MAX_DEGREE 101

typedef struct {
    int degree;               // 최대 차수
    float x_coef[MAX_DEGREE]; // x 계수 배열
    float y_coef[MAX_DEGREE]; // y 계수 배열
} extended_polynomial;

typedef struct {
    int x_exp;  // x의 차수
    int y_exp;  // y의 차수
    float coef; // 항의 계수
} term;

// term 배열에서 y의 차수에 따라 내림차순 정렬
int compare(const void* a, const void* b) {
    term* termA = (term*)a;
    term* termB = (term*)b;

    // y의 차수로 정렬하되, 동일한 경우 x 차수를 비교
    if (termB->y_exp != termA->y_exp) {
        return termB->y_exp - termA->y_exp;
    }
    else {
        return termB->x_exp - termA->x_exp;  // x 차수에 대해 내림차순
    }
}

// 다항식 곱셈 함수
void multiply_polynomials(extended_polynomial* a, extended_polynomial* b, term* result, int* term_count) {
    int count = 0;

    for (int i = 0; i <= a->degree; i++) {
        for (int j = 0; j <= b->degree; j++) {
            if ((a->x_coef[i] != 0 || a->y_coef[i] != 0) && (b->x_coef[j] != 0 || b->y_coef[j] != 0)) {
                // x 항 곱하기
                if (a->x_coef[i] != 0 && b->x_coef[j] != 0) {
                    result[count].coef = a->x_coef[i] * b->x_coef[j];
                    result[count].x_exp = i + j;
                    result[count].y_exp = 0;
                    count++;
                }
                // y 항 곱하기
                if (a->y_coef[i] != 0 && b->y_coef[j] != 0) {
                    result[count].coef = a->y_coef[i] * b->y_coef[j];
                    result[count].x_exp = 0;
                    result[count].y_exp = i + j;
                    count++;
                }
                // x*y 혼합 항 곱하기
                if (a->x_coef[i] != 0 && b->y_coef[j] != 0) {
                    result[count].coef = a->x_coef[i] * b->y_coef[j];
                    result[count].x_exp = i;
                    result[count].y_exp = j;
                    count++;
                }
                if (a->y_coef[i] != 0 && b->x_coef[j] != 0) {
                    result[count].coef = a->y_coef[i] * b->x_coef[j];
                    result[count].x_exp = j;
                    result[count].y_exp = i;
                    count++;
                }
            }
        }
    }
    *term_count = count;
}

// 다항식 출력 함수 (x^0이나 y^0 처리)
void print_polynomial(term* terms, int term_count) {
    int first = 1;
    for (int i = 0; i < term_count; i++) {
        if (terms[i].coef == 0) continue; // 계수가 0인 항은 생략

        // 부호 출력
        if (!first && terms[i].coef > 0) {
            printf("+");
        }

        // 상수항 처리
        if (terms[i].y_exp == 0 && terms[i].x_exp == 0) {
            printf("%.1f", terms[i].coef);  // 상수 출력
        }
        else if (terms[i].y_exp == 0) {
            printf("%.1fx^%d", terms[i].coef, terms[i].x_exp);  // y^0 생략
        }
        else if (terms[i].x_exp == 0) {
            printf("%.1fy^%d", terms[i].coef, terms[i].y_exp);  // x^0 생략
        }
        else {
            printf("%.1fy^%dx^%d", terms[i].coef, terms[i].y_exp, terms[i].x_exp);
        }

        first = 0;
    }
    printf("\n");
}

int main() {
    // 다항식 초기화 (test case 3)
    extended_polynomial a1 = { 7, {-1, 0, 0, 0, 4, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 3} };
    extended_polynomial b1 = { 4, {7, 0, 0, 0, 5}, {0, 0, -3, 0, 0} };


    // 결과를 저장할 배열
    term result[MAX_DEGREE * MAX_DEGREE];
    int term_count;

    // 다항식 곱셈
    multiply_polynomials(&a1, &b1, result, &term_count);

    // y의 차수에 대해 내림차순 정렬
    qsort(result, term_count, sizeof(term), compare);

    // 결과 출력
    printf("결과 다항식: ");
    print_polynomial(result, term_count);

    return 0;
}

 

 

 

#include <stdio.h>
#include <stdlib.h>

#define MAX_DEGREE 101


typedef struct {
	int x_degree;	//다항식의 하나의 항에서의 x의 차수
	int y_degree;	//다항식의 하나의 항에서의 y의 차수
	int coef;	//다항식의 하나의 항에서의 계수
}term;			//다항식중에서 하나의 항을 나타내는 구조체

typedef struct {
	term terms[MAX_DEGREE];	//다항식의 항 별 요소(term 구조체 배열 : x의 차수,y의 차수,계수)
	int terms_count;		//다항식의 전체 항 개수
}polynomial;				//다항식은 여러 항으로 구성되어 있으므로 각 항들의 요소(x,y의 차수,항 별 계수)와 전체 항의 개수를 포함하는 구조체

int compare(const void* a, const void* b) {
	term* termA = (term*)a;
	term* termB = (term*)b;
	if (termA->y_degree != termB->y_degree) {
		return termB->y_degree - termA->y_degree; 
	}
	else {
		return termB->x_degree - termA->x_degree; 
	}
}


polynomial mult_Poly(polynomial a, polynomial b)
{
	polynomial c;
	c.terms_count = 0; //항의 개수 0으로 초기화
	//각 항별 곱셈 진행
	for (int i = 0; i < a.terms_count; i++) {
		for (int j = 0; j < b.terms_count; j++) {
			term temp_term;	
			
			temp_term.coef = a.terms[i].coef * b.terms[j].coef;
			temp_term.x_degree = a.terms[i].x_degree + b.terms[j].x_degree;
			temp_term.y_degree = a.terms[i].y_degree + b.terms[j].y_degree;
			c.terms[c.terms_count++] = temp_term;
		}
	}
	//차수가 같은 항 계수 정리
	for (int i = 0; i < c.terms_count; i++) {
		for (int j = i + 1; j < c.terms_count; j++) {
			if (c.terms[i].x_degree == c.terms[j].x_degree && c.terms[i].y_degree == c.terms[j].y_degree) {
				c.terms[i].coef += c.terms[j].coef;
				//j번째 항 삭제 (한칸 앞으로 밀어 덮어씌움)
				for (int k = j; k < c.terms_count - 1; k++) {
					c.terms[k] = c.terms[k + 1];
				}
				c.terms_count--;
				j--;
			}
		}
	}
	qsort(c.terms, c.terms_count, sizeof(term), compare);
	return c;
}

void print_Poly(polynomial p)
{
	for (int i = 0; i < p.terms_count; i++) {
		if (p.terms[i].coef != 0) {
			if (p.terms[i].coef > 0) { printf("+"); }
			printf("%d", p.terms[i].coef);
			if (p.terms[i].y_degree > 0) {
				printf("y^%d",p.terms[i].y_degree);
			}
			if (p.terms[i].x_degree > 0) {
				printf("x^%d", p.terms[i].x_degree);
			}
		}
	}
	printf("\n");
}

int main() {

	polynomial a1 = { { {0, 7, 3}, {4, 0, 4}, {0, 0, -1} }, 3 };  
	polynomial b1 = { { {4, 0, 5}, {0, 2, -3}, {0, 0, 7} }, 3 };  
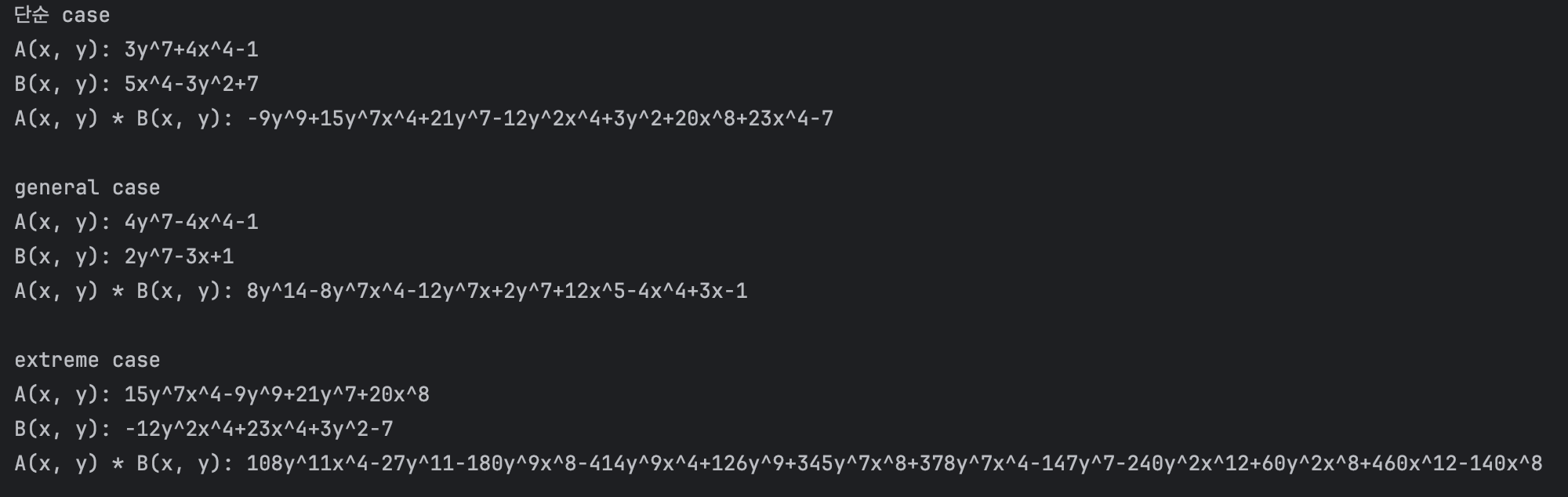
	printf("단순 case\n");
	print_Poly(a1);
	print_Poly(b1);
	printf("-------------------------------------------------------------------------------------------------------------\n");
	polynomial result1 = mult_Poly(a1, b1);
	print_Poly(result1);

	
	polynomial a2 = { { {0, 7, 4}, {4, 0, -4}, {0, 0, -1} }, 3 };  
	polynomial b2 = { { {0, 7, 2}, {1, 0, -3}, {0, 0, 1} }, 3 };  
	printf("\ngeneral case\n");
	print_Poly(a2);
	print_Poly(b2);
	printf("-------------------------------------------------------------------------------------------------------------\n");
	polynomial result2 = mult_Poly(a2, b2);
	print_Poly(result2);

	
	polynomial a3 = { { {4, 7, 15}, {0, 9, -9}, {0, 7, 21}, {8, 0, 20} }, 4 };  
	polynomial b3 = { { {4, 2, -12}, {4, 0, 23}, {0, 2, 3}, {0, 0, -7} }, 4 };  
	printf("\nextreme case\n");
	print_Poly(a3);
	print_Poly(b3);
	printf("-------------------------------------------------------------------------------------------------------------\n");
	polynomial result3 = mult_Poly(a3, b3);
	print_Poly(result3);

	return 0;
}

#include <stdio.h>
#include <stdlib.h>

#define MAX_DEGREE 101
#define MAX(a,b) (((a)>(b))?(a):(b))

typedef struct {
    int x_exp;  // x의 차수
    int y_exp;  // y의 차수
    int coef;   // 계수 (정수로 변경)
} term;

typedef struct {
    term terms[MAX_DEGREE];
    int term_count; //곱셈을 위한 항의개수
} polynomial;

// 비교 함수: y 차수를 기준으로 내림차순 정렬, y 차수가 같으면 x 차수 내림차순
int compare(const void* a, const void* b) {
    term* term_a = (term*)a;
    term* term_b = (term*)b;

    if (term_a->y_exp != term_b->y_exp)
        return term_b->y_exp - term_a->y_exp;  // y 차수에 대해 내림차순
    return term_b->x_exp - term_a->x_exp;      // y 차수가 같으면 x 차수에 대해 내림차순
}

// 다항식의 곱 함수
polynomial multPoly(polynomial a, polynomial b) {
    polynomial c;
    c.term_count = 0;

    // 각 항을 곱함
    for (int i = 0; i < a.term_count; i++) {
        for (int j = 0; j < b.term_count; j++) {
            term new_term;      //새로운항을 만들고 한번 곱셈하여 저장함
            new_term.coef = a.terms[i].coef * b.terms[j].coef;
            new_term.x_exp = a.terms[i].x_exp + b.terms[j].x_exp;
            new_term.y_exp = a.terms[i].y_exp + b.terms[j].y_exp;

            // 동일한 차수가 있으면 계수를 합산
            int found = 0;
            for (int k = 0; k < c.term_count; k++) {
                if (c.terms[k].x_exp == new_term.x_exp && c.terms[k].y_exp == new_term.y_exp) {
                    c.terms[k].coef += new_term.coef;
                    found = 1;
                    break;
                }
            }

            if (!found) {
                c.terms[c.term_count++] = new_term;
            }
        }
    }

    // qsort를 이용하여 y 차수를 기준으로 내림차순 정렬
    qsort(c.terms, c.term_count, sizeof(term), compare);

    return c;
}

// 다항식 출력 함수
void printPoly(polynomial p) {
    for (int i = 0; i < p.term_count; i++) {
        if (p.terms[i].coef != 0) {
            if (i > 0 && p.terms[i].coef > 0) printf("+");
            printf("%d", p.terms[i].coef);  // 계수를 정수로 출력

            if (p.terms[i].y_exp > 0) {
                printf("y");
                if (p.terms[i].y_exp > 1) printf("^%d", p.terms[i].y_exp);
            }

            if (p.terms[i].x_exp > 0) {
                printf("x");
                if (p.terms[i].x_exp > 1) printf("^%d", p.terms[i].x_exp);
            }
        }
    }
    printf("\n");
}

int main() {
    // 단순 case
    polynomial a1 = {{ {0, 7, 3}, {4, 0, 4}, {0, 0, -1} }, 3};  // 3y^7 + 4x^4 - 1
    polynomial b1 = {{ {4, 0, 5}, {0, 2, -3}, {0, 0, 7} }, 3};  // 5x^4 - 3y^2 + 7

    printf("단순 case\nA(x, y): ");
    printPoly(a1);
    printf("B(x, y): ");
    printPoly(b1);
    polynomial result1 = multPoly(a1, b1);
    printf("A(x, y) * B(x, y): ");
    printPoly(result1);

    // general case
    polynomial a2 = {{ {0, 7, 4}, {4, 0, -4}, {0, 0, -1} }, 3};  // 4y^7 - 4x^4 - 1
    polynomial b2 = {{ {0, 7, 2}, {1, 0, -3}, {0, 0, 1} }, 3};   // 2y^7 - 3x + 1

    printf("\ngeneral case\nA(x, y): ");
    printPoly(a2);
    printf("B(x, y): ");
    printPoly(b2);
    polynomial result2 = multPoly(a2, b2);
    printf("A(x, y) * B(x, y): ");
    printPoly(result2);

    // extreme case
    polynomial a3 = {{ {4, 7, 15}, {0, 9, -9}, {0, 7, 21}, {8, 0, 20} }, 4};  // 15x^4y^7 -9y^9 +21y^7 +20x^8
    polynomial b3 = {{ {4, 2, -12}, {4, 0, 23}, {0, 2, 3}, {0, 0, -7} }, 4};  // -12x^4y^2 +23x^4 +3y^2 -7

    printf("\nextreme case\nA(x, y): ");
    printPoly(a3);
    printf("B(x, y): ");
    printPoly(b3);
    polynomial result3 = multPoly(a3, b3);
    printf("A(x, y) * B(x, y): ");
    printPoly(result3);

    return 0;
}

다항식 곱셈기

 

 

polynomial poly_add1(polynomial a,polynomial b) {
    polynomial c;
    int Apos=0,Bpos=0,Cpos=0;
    int degree_a=a.degree,degree_b=b.degree;
    c.degree=MAX(a.degree,b.degree);

    while(Apos<=degree_a && Bpos<=degree_b) {
        if(degree_a>degree_b) {
            //A항>B항
            c.coef[Cpos++]=a.coef[Apos++];  //c다항식에
            degree_a--;
        }
        else if(degree_b==degree_a) {
            c.coef[Cpos++]=b.coef[Bpos++];
            degree_b--;
            degree_a--;
        }
        else {
            c.coef[Cpos++]=b.coef[Bpos++];
            degree_b--;
        }
    }
    return c;
}

 

다항식 덧셈기

 

#include <stdio.h>
#include <stdlib.h>
#define MAX_DEGREE 101
#define MAX(a,b) (((a)>(b))?(a):(b))
typedef struct {
    int degree;
    float coef[MAX_DEGREE];
}polynomial;


polynomial poly_subtract (polynomial a,polynomial b) {
    polynomial result;
    int Apos=0,Bpos=0,Cpos=0;
    int degree_a=a.degree;
    int degree_b=b.degree;
    result.degree=MAX(a.degree,b.degree);
while(Apos<=a.degree&&Bpos<=b.degree) {
    if(degree_a>degree_b) {
        result.coef[Cpos++]=a.coef[Apos++];
        degree_a--;
    }
    else if(degree_a==degree_b) {
        result.coef[Cpos++]=a.coef[Apos++]-b.coef[Bpos++];
        degree_a--,degree_b--;
    }
    else {
        result.coef[Cpos++]=b.coef[Bpos++];
        degree_b--;
        }
    }
return result;
}

void print_poly(polynomial p) {
    for(int i=p.degree;i>0;i--) {
        printf("%3.1fx^%d + ",p.coef[p.degree-i],i);
    }
    printf("%3.1f \n",p.coef[p.degree]);
}

int main(void){
    polynomial a={5,{3,6,0,0,0,10}};
    polynomial b={4,{7,0,5,0,1}};
    polynomial c;
    print_poly(a);
    print_poly(b);
    c=poly_subtract(a,b);
    printf("-------------------------------------------------------------\n\n");
    print_poly(c);
    return 0;
}

다항식 뺄셈기

 

 

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define _CRT_SECURE_NO_WARNGINS
#define MAX 101
 
//두 다항식 입력받고 배열에 저장 (계수따로 지수따로)//
//최대지수는 100으로 한정, 계수와 변수사이는 *없이 그냥 입력받으며 지수의경우 ^으로 구분//
//두 다항식간의 사칙연산 함수 입력// 
//다항식은 내림차순으로 입력//
//변수 이름에 한글을 쓸 시 에러가 발생하기에, 영어로 작성//
//1. subTerm = 다항식 - 다항식//
//2. addTerm = 다항식 + 다항식//
//3. delTerm = 입력했던 다항식 초기화//
//4. MultPoly = 다항식 × 다항식//
//5. exit = 종료// 

typedef struct {
    int expo; //최대 지수값
    int coef[MAX]; //최대지수 101로 한정
}poly;
 
 
void show(poly A) // 해당 다항식 출력
{
 
    for (int i = 0; i<A.expo; i++) {
        if (A.coef[i] != 0)
            printf("%dx^%d", A.coef[i], A.expo - i);
        if (A.coef[i + 1] >= 0 && A.coef[i] != 0)
            printf(" + ");
 
    }
    printf("%d ", A.coef[A.expo]);
 
}
 
poly polynomialSave()
{
    poly C;
    memset(&C, 0, sizeof(C));
    int num1, num2;
    printf("최고차항을 입력해주세요.\n");
    scanf("%d", &num1);
    C.expo = num1;
    for (int i = 0; i <= num1; i++)
    {
        printf("x^%d의 계수를 입력해주세요.\n", num1 - i);
        scanf("%d", &num2);
        C.coef[i] = num2;
    }
    return C;
}


 
poly subPoly(poly A) 
{
    poly B;
    B = polynomialSave();
 
    poly C;
 
 
    int indxA = 0, indxB = 0, indxC = 0, degA = A.expo, degB = B.expo;
 
    C.expo = (A.expo>B.expo) ? A.expo : B.expo;//최고차항 저장
 
    while (A.expo >= indxA && B.expo >= indxB)//각 항의 최고차항을 이용해 연산
    {
        if (degA == degB)
        {
            C.coef[indxC++] = A.coef[indxA++] - B.coef[indxB++];
 
            degA--; degB--;
        }
        else if (degA>degB)
        {
            C.coef[indxC++] = A.coef[indxA++];
            degA--;
        }
        else
        {
            C.coef[indxC++] = B.coef[indxB++];
            degB--;
        }
 
    }
 
    printf("    ");
    show(A);
    printf("\n %c  ", '-');
    show(B);
    printf("\n  = ");
    show(C);
    printf("\n");
 
    return C;
}
 
poly addPoly(poly A)
{
    poly B;
    B = polynomialSave();
 
    poly C;
 
 
    int indxA = 0, indxB = 0, indxC = 0, degA = A.expo, degB = B.expo;
 
    C.expo = (A.expo>B.expo) ? A.expo : B.expo;//최고차항 저장
 	
    while (A.expo >= indxA && B.expo >= indxB)// 각항의 최고차항을 이용해 연산
    {
        if (degA == degB)
        {
            C.coef[indxC++] = A.coef[indxA++] + B.coef[indxB++];
            degA--; degB--;
        }
        else if (degA>degB)
        {
            C.coef[indxC++] = A.coef[indxA++];
            degA--;
        }
        else
        {
            C.coef[indxC++] = B.coef[indxB++];
            degB--;
        }
 
    }
 
    printf("    ");
    show(A);
    printf("\n %c  ", '+');
    show(B);
    printf("\n  = ");
    show(C);
    printf("\n");
    return C;
}
 
poly delTerm(poly A)
{
    printf("다항식값을 초기화합니다.\n");
    memset(&A, 0, sizeof(A));
 
    return A;
}
 
poly MultPoly(poly A)
{
    poly B;
    B = polynomialSave();
 
    poly C;
 
    memset(&C, 0, sizeof(C));
    int indxA = 0, indxB = 0, indxC = 0, degA = A.expo, degB = B.expo;
 
    C.expo = A.expo + B.expo;//최고차항은 A,B의 최고차항의 합이다.
 
    for (int i = 0; i <= A.expo; i++)
    {
        for (int j = 0; j <= B.expo; j++)
        {
            C.coef[i + j] += A.coef[i] * B.coef[j];
        }
    }
    printf("    ");
    show(A);
    printf("\n %c  ", '*');
    show(B);
    printf("\n  = ");
    show(C);
    printf("\n");
 
    return C;
}

 void menu(poly A)
{
    int num = 0;
    while (1)
    {
        printf("1.SubPoly 2.AddPoly 3.DelTerm 4.MultPoly 5.Exit \n");
        scanf("%d", &num);
 
        if (num == 6)
            break;
        switch (num)
        {
        case 1:
            A = subPoly(A);
            break;
 
        case 2:
            A = addPoly(A);
            break;
        case 3:
            delTerm(A);
            A = polynomialSave();
            break;
        case 4:
            MultPoly(A);
            break;
        
        default:
            printf("정확한 값을 넣어주세요.\n");
        }
        puts("");
    }
}
int main()
{
    poly A;
    A = polynomialSave();
    menu(A);
    printf("프로그램을 종료합니다.\n");
    return 0;
}
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define MAX_TERMS 100      /* 항 배열의 크기*/

typedef struct {
    float coef;
    int expon;
} polynomial;

polynomial terms[MAX_TERMS];
int avail = 0;

void attach(float coefficient, int exponent)
{             /* 새로운 항을 다항식에 첨가한다. */
    if (avail >= MAX_TERMS) {
        printf(" 다항식에 항이 너무 많다.");
        exit(1);
    }
    terms[avail].coef = coefficient;
    terms[avail++].expon = exponent;
}

void attach2(float coefficient, int exponent, int s)   //같은 지수의 계수 더하기
{
    /*  곱셈한 항을 다항식에 첨가 */
    int i;
    int j;

    if (avail >= MAX_TERMS) {
        printf("다항식에 항이 너무 많다.");
        exit(1);
    }
    avail--;

    i = avail;

    for (j = i; j >= s; j--)
    {
        if (terms[j].expon == exponent)         //지수가 같을 경우 계수를 더해줌
        {
            terms[j].coef += coefficient;
            avail++;
            return;
        }
        else
            break;
        //지수가 같지 않을 경우 그냥 다항식에 첨가
    }
    avail++;
    terms[avail].coef = coefficient;
    terms[avail++].expon = exponent;
}

void print(int start, int finish)
{
    int i;
    printf("\n");

    if (start <= finish) {
        for (i = start; i < finish; i++)
            printf("%3.1f x^ %d + ", terms[i].coef, terms[i].expon);
        // 마지막 항을 출력
        printf("%3.1f x^ %d \n", terms[finish].coef, terms[finish].expon);
    }
    else
        printf(" No terms ");

}


void pmult(int starta, int finisha, int startb, int finishb, int* startd, int* finishd)
{  /* A(x)와 B(x)를 곱하여 D(x)를 생성한다. */
    float coefficient;
    int exponent;
    int i, j;
    int s;

    *startd = avail;

    for (i = starta; i <= finisha; i++)
    {
        for (j = startb; j <= finishb; j++)
        {
            coefficient = terms[i].coef * terms[j].coef;   //계수의 곱
            exponent = terms[i].expon + terms[j].expon;  // 지수의 합
            s = finisha + finishb;                        // s의 위치 지정
            attach2(coefficient, exponent, s);          //곱셈항 첨가   
        }
    }

    *finishd = avail - 1;

}

int main(int argc, char* argv[])
{

    int startA, finishA;  // 다항식 A
    int startB, finishB;  // 다항식 B
    int startC, finishC;  // 다항식 C

    int i, n, e;
    float c;

    printf("다항식의 곱셈 연산 수행!\n");
    printf("다항식 A의 항의 수 : ");
    scanf("%d", &n);

    startA = avail;
    for (i = 1; i <= n; i++) {
        printf("\n다항식 A의 %d 번째 항의 계수와 지수 : ", i);
        scanf("%f%d", &c, &e);

        attach(c, e);
    }
    finishA = avail - 1;

    print(startA, finishA);   // 다항식 A의 입력결과

    printf("\n다항식 B의 항의 수 : ");
    scanf("%d", &n);

    startB = avail;
    for (i = 1; i <= n; i++) {
        printf("\n다항식 B의 %d 번째 항의 계수와 지수 : ", i);
        scanf("%f%d", &c, &e);

        attach(c, e);
    }
    finishB = avail - 1;

    print(startB, finishB);    // 다항식 b의 입력결과

    pmult(startA, finishA, startB, finishB, &startC, &finishC);   // 곱셈

    printf(" \n 곱셈의 결과 : ");
    print(startC, finishC);   // 곱셈 결과 출력

    return 0;
}

'DSA' 카테고리의 다른 글

회문(Palindrome) 검사 (스택)  (1) 2024.10.27
스택 2개를 이용한 선형 큐의 구현  (0) 2024.10.25
리스트 1 (ArrayList)  (0) 2024.08.26
큐(Queue) 활용 예제  (0) 2024.08.26
덱(Deque) 2  (0) 2024.08.25

관련글

티스토리툴바